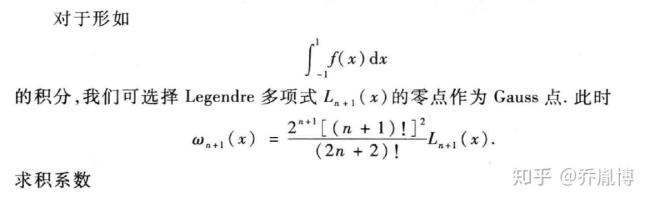根据高斯型求积公式∫1-1f(x)dx≈ nr=1Arf(xr)的最大代数精确度,利用正交条件推出n=3的高斯型求积公式∫1-1f(x)dx≈59f(-35)+89f(0)+59f(35)。
由于Gauss型求积公式属于数值积分的内容,学东西总要知道它的来龙去脉,下面我简单介绍一下为什么要引入数值积分
给定函数f ( x ) ∈ C [ a , b ] f(x)in C[a,b]f(x)∈C[a,b],考虑积分
I ( f ) = ∫ a b f ( x ) d x I(f)=int_{a}^{b} f(x) dx
I(f)=∫
a
b
f(x)dx
的计算问题,从数学分析中知道,当已知f ( x ) f(x)f(x)的原函数为F ( x ) F(x)F(x)时,由牛顿-莱布尼兹公式,有
I ( f ) = ∫ a b f ( x ) d x = F ( b ) − F ( a ) I(f)=int_{a}^{b}f(x)dx=F(b)-F(a)
I(f)=∫
a
b
f(x)dx=F(b)−F(a)
然而,在实际计算中,被积函数的f ( x ) f(x)f(x)的原函数经常无法用初等函数表示,但过于复杂。还有时,f ( x ) f(x)f(x)只在一些离散点上给出。在这样的情况下,就有必要借助数值方法来求I ( f ) I(f)I(f)的近似值。