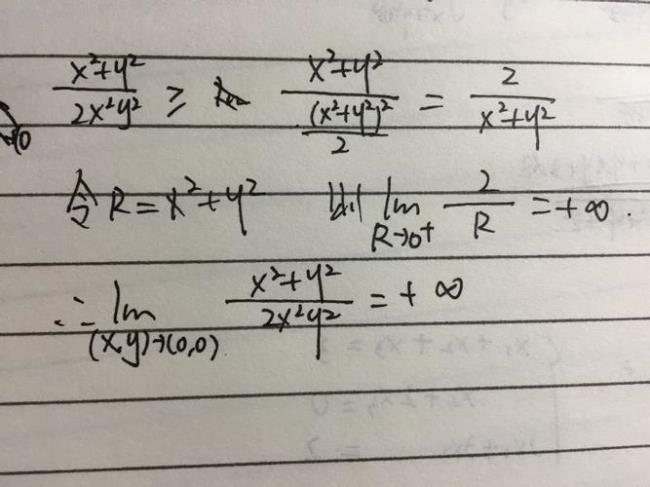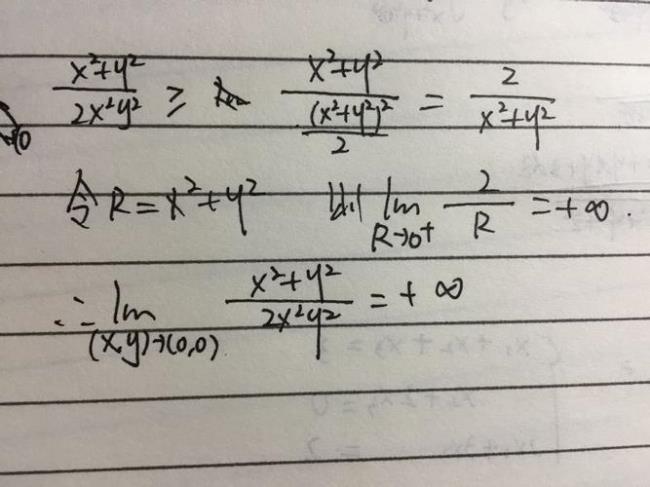设y=x²,则f(x,y)=x³/(x²+x^8)。
由于当x→0时,x^8相对于x²是高阶无穷小,可忽略。则有:
f(x,y)=x³/x²=x=0
再设y=x^(¼),则f(x,y)=x^(3/2)/(x²+x)。
当x→0时,x²相对于x是高阶无穷小,可忽略。则有
f(x,y)=x^(3/2)/x=x^(1/2)=0
在以上两种情况下,f(x,y)的极限为0。
可是若设y=x^(0.5)或y=√x,则
f(x,y)=x²/(x²+x²)=1/2。
此时x→0时,f(x,y)是一个常数。
你的问题是:“那条曲线上的点都可以找到那些直线上的点一一对应,为什么最后他的极限不为0,难道曲线上有点是无法在直线上找到的吗”
现在我们看看什么直线(y=kx)与这条曲线(y=√x)在趋近0时是一致的。显然,这条直线必须是此曲线在x=0时的切线。
由于曲线y=√x的一阶导数是:
y′=1/(2√x)
所以此曲线在x=0处切线的斜率是无穷大(k=∞)。由于(k=∞),除x=0外,任何一个非0的x值都会使y值无穷大。这样,除x=0外,曲线y=√x上的点确实无法在此直线上找到一个对应的近似值。这样你的问题所得到的回答是肯定的。