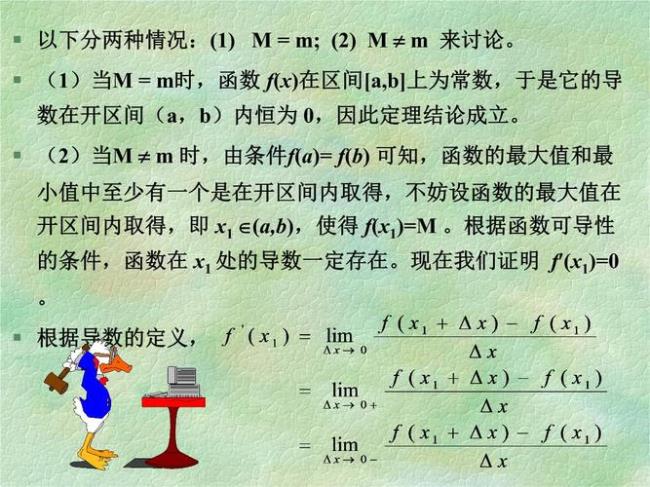
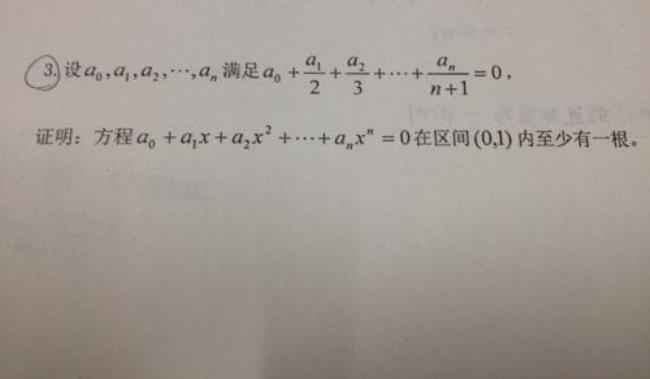①若要证明 ,则考虑直接使用罗尔定理,无需构造辅助函数。
例:
设 (其中 均为常数),证:方程 在 内至少有一个解。
思路:经过端点的带入尝试,你会发现无法直接找到函数的零点,因此我们选择求其原函数的两个零点,从而达到我们想要的效果。
解: 令 。
由罗尔定理可得: 即原方程至少存在一个解得证。
②若要证明 ,则考虑构造辅助函数 ,然后使用罗尔定理即可。
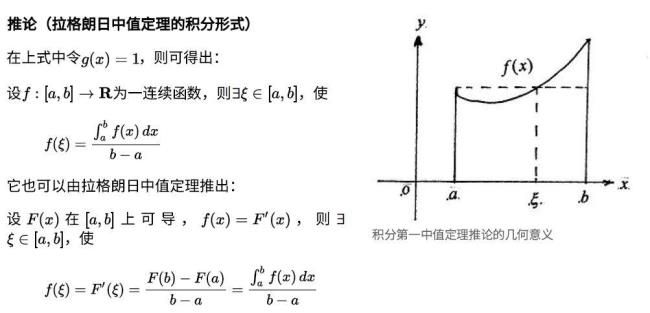
此方法可以用来证明拉格朗日中值定理,具体证明见中值定理基础篇。
③若要证明 或者 ,则考虑多次使用罗尔定理。
例1:
设 三阶可导, ,证明:
解:
由于 ,所以由罗尔定理可得: .
因此,可以得到 ,进行两次罗尔定理可得 。 最后,再对 使用一次罗尔定理可得 ,由此得证。
例2:
设 上三阶可导, ,证明:
思路:虽然这道题没有足够多的零点,但是函数是具体的,可以自行求导寻找零点和驻点。
解:由于 使用罗尔定理可得 。
由 可得: 对 使用罗尔定理可得 ,由此得证。
例3:
设 二阶可导, ,证明:
思路:要求二阶导为0,则需要三个 零点,题目已经给出两个,因此我们只需要从第三个条件中推出一个零点即可。
解:不妨假设,
又由于 在 上二阶可导, 由零点定理
到此,我们得到了三个零点,反复使用罗尔定理就可以得到所证结论。
例4:
设 在 上连续,且 证明: 在 内至少有两个零点。
常见的错误解法:直接使用积分中值定理
错解: ,从而由此得到 两个零点,但是实际上这是错误的,因为我们无法确定 与 是否相等。 正确解法:
思路:既然我们无法直接找到函数的两个零点,那么我们可以退而求其次的找其原函数的三个零点,从而达到我们想要的效果。 解:令 ,则 .
由于 再由积分中值定理得 。到此我们得到了三个零点,只需反复使用罗尔定理,就可以得到需证结论。