运用公式
设P为椭圆上的任意一点
角F1F2P=α ,F2F1P=β,F1PF2=θ
则有离心率e=sin(α+β) / (sinα+sinβ)
焦点三角形面积S=b^2*tan(θ/2).
证明方法一
设F1P=m ,F2P=n ,2a=m+n
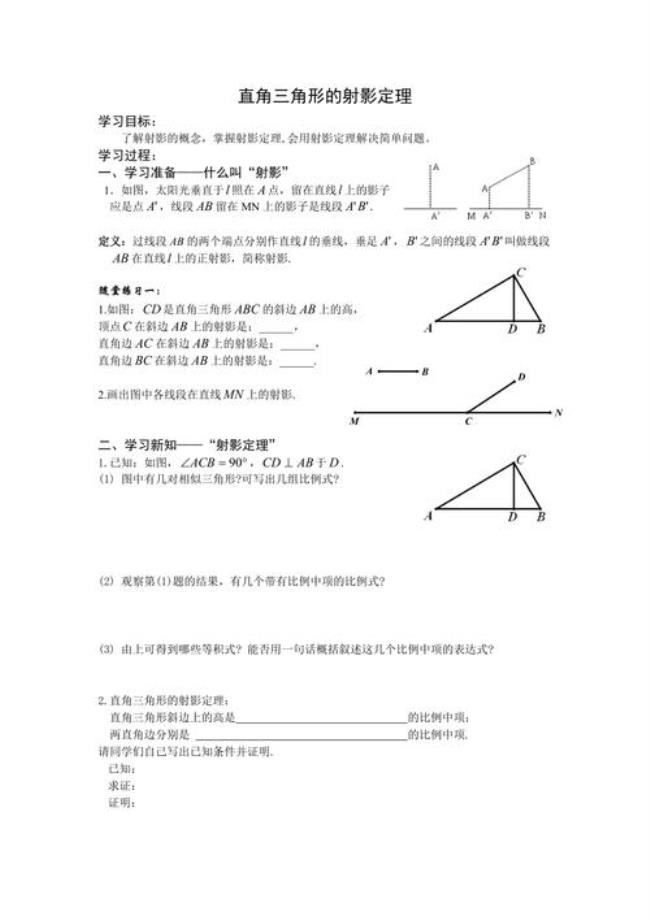
由射影定理得2c=mcosβ+ncosα
e=c/a=2c/2a=mcosβ+ncosα / (m+n)
由正弦定理e=sinαcosβ+sinβcosα/ (sinβ+sinα)=sin(α+β)/ (sinα + sinβ).
证明方法二
对于焦点△F1PF2,设PF1=m,PF2=n
则m+n=2a
在△F1PF2中,由余弦定理:
(F1F2)^2=m^2+n^2-2mncosθ
即4c^2=(m+n)^2-2mn-2mncosθ=4a^2-2mn(1+cosθ)
所以mn(1+cosθ)=2a^2-2c^2=2b^2
所以mn=2b^2/(1+cosθ)
S=(mnsinθ)/2.(正弦定理的三角形面积公式)
=b^2*sinθ/(1+cosθ)
=b^2*[2sin(θ/2)cos(θ/2)]/2[cos(θ/2)]^2
=b^2*sin(θ/2)/cos(θ/2)
=b^2*tan(θ/2)